>>> protein_data = pd.DataFrame.from_csv('../data/protein_classification.csv')
>>> X = protein_data['Sequence']
>>> def split(word): 
>>>    return [char for char in word]>>> sequences = [split(x) for x in X]
>>> print(sequences[0])
['M', 'E', 'I', 'E', 'K', 'T', 'N', 'R', 'M', 'N', 'A', 'L', 'F', 'E', 'F', 'Y', 'A', 'A', 'L', 'L', 'T', 'D', 'K', 'Q', 'M', 'N', 'Y', 'I', 'E', 'L', 'Y', 'Y', 'A', 'D', 'D', 'Y', 'S', 'L', 'A', 'E', 'I', 'A', 'E', 'E', 'F', 'G', 'V', 'S', 'R', 'Q', 'A', 'V', 'Y', 'D', 'N', 'I', 'K', 'R', 'T', 'E', 'K', 'I', 'L', 'E', 'D', 'Y', 'E', 'M', 'K', 'L', 'H', 'M', 'Y', 'S', 'D', 'Y', 'I', 'V', 'R', 'S', 'Q', 'I', 'F', 'D', 'Q', 'I', 'L', 'E', 'R', 'Y', 'P', 'K', 'D', 'D', 'F', 'L', 'Q', 'E', 'Q', 'I', 'E', 'I', 'L', 'T', 'S', 'I', 'D', 'N', 'R', 'E']

Next, we generate the sequence embeddings.

>>> from sgt import Sgt
>>> sgt = Sgt(kappa = 10, lengthsensitive = False)
>>> embedding = sgt.fit_transform(corpus=sequences)

The embedding is in 400-dimensional space. Let’s first do PCA on it and reduce the dimension to two. This will also help visualize the clusters.

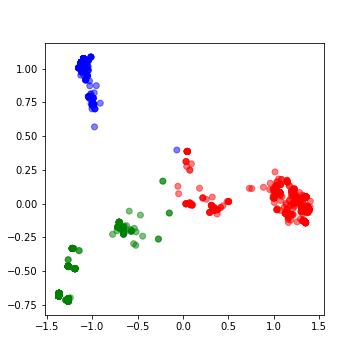
Moving on to building classifiers.

Classification

Protein Sequence Classification

We will start by building a classifier on the same protein dataset we used earlier. The proteins in the dataset have two functions. Therefore, we will build a binary classifier.

We will first convert the:

function [CC]

a column in the data into labels that can be ingested in an MLP model built-in

keras

>>> y = protein_data['Function [CC]']
>>> encoder = LabelEncoder()
>>> encoder.fit(y)
>>> encoded_y = encoder.transform(y)

In the following, we build the MLP classifier and run 10-fold cross-validation.

>>> kfold = 10
>>> X = pd.DataFrame(embedding)
>>> y = encoded_y>>> random_state = 1>>> test_F1 = np.zeros(kfold)
>>> skf = KFold(n_splits = kfold, shuffle = True, random_state = random_state)
>>> k = 0
>>> epochs = 50
>>> batch_size = 128>>> for train_index, test_index in skf.split(X, y):
>>>     X_train, X_test = X.iloc[train_index], X.iloc[test_index]
>>>     y_train, y_test = y[train_index], y[test_index]
>>>     X_train = X_train.as_matrix(columns = None)
>>>     X_test = X_test.as_matrix(columns = None)
>>>     
>>>     model = Sequential()
>>>     model.add(Dense(64, input_shape = (X_train.shape[1],), init = 'uniform')) 
>>>     model.add(Activation('relu'))
>>>     model.add(Dropout(0.5))
>>>     model.add(Dense(32, init='uniform'))
>>>     model.add(Activation('relu'))
>>>     model.add(Dropout(0.5))
>>>     model.add(Dense(1, init='uniform'))
>>>     model.add(Activation('sigmoid'))
>>>     model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
>>>     
>>>     model.fit(X_train, y_train ,batch_size=batch_size, epochs=epochs, verbose=0)
>>>     
>>>     y_pred = model.predict_proba(X_test).round().astype(int)
>>>     y_train_pred = model.predict_proba(X_train).round().astype(int)>>>     test_F1[k] = sklearn.metrics.f1_score(y_test, y_pred)
>>>     k+=1
    
>>> print ('Average test f1-score', np.mean(test_F1))
Average test f1-score 1.0

This data turns out to be too good for the classifier. We have another dataset that is more challenging. Let’s go over it.

Network Log Data Classification

This data sample is taken from here. This is a network intrusion data containing audit logs and any attack as a positive label. Since network intrusion is a rare event, the data is unbalanced. Additionally, we have a small dataset of only 111 records. Here we will build a sequence classification model to predict a network intrusion.

Each sequence contains in the data is a series of activity, for example, 

{login, password, …}

The alphabets in the input data sequences are already encoded into integers. The original sequences data file is present here.

Similar to before, we will first prepare the data for a classifier.

>>> darpa_data = pd.DataFrame.from_csv('../data/darpa_data.csv')
>>> X = darpa_data['seq']
>>> sequences = [x.split('~') for x in X]>>> y = darpa_data['class']
>>> encoder = LabelEncoder()
>>> encoder.fit(y)
>>> y = encoder.transform(y)

In this data, the sequence embeddings should be length-sensitive. The lengths are important here because sequences with similar patterns but different lengths can have different labels. Consider a simple example of two sessions: 

{login, pswd, login, pswd,…}
{login, pswd,…(repeated several times)…, login, pswd}

While the first session can be a regular user mistyping the password once, the other session is possibly an attack to guess the password. Thus, the sequence lengths are as important as the patterns.

>>> sgt_darpa = Sgt(kappa = 5, lengthsensitive = True)
>>> embedding = sgt_darpa.fit_transform(corpus=sequences)

The embedding we find here is sparse. Therefore, we will perform dimension reduction using PCA before we train a classifier.

>>> from sklearn.decomposition import PCA
>>> pca = PCA(n_components=35)
>>> pca.fit(embedding)
>>> X = pca.transform(embedding)
>>> print(np.sum(pca.explained_variance_ratio_))
0.9862350164327149

The selected top-35 PCAs are explaining more than 98% of the variance. We will now go ahead and build a Multi-Layer Perceptron using keras. Since the data size is small and, also, the number of positive labeled points, we will perform a 3-fold validation.

>>> kfold = 3
>>> random_state = 11>>> test_F1 = np.zeros(kfold)
>>> time_k = np.zeros(kfold)
>>> skf = StratifiedKFold(n_splits=kfold, shuffle=True, random_state=random_state)
>>> k = 0
>>> epochs = 300
>>> batch_size = 15>>> class_weight = {0 : 0.12, 1: 0.88,}  # The weights can be changed and made inversely proportional to the class size to improve the accuracy.>>> for train_index, test_index in skf.split(X, y):
>>>     X_train, X_test = X[train_index], X[test_index]
>>>     y_train, y_test = y[train_index], y[test_index]
>>>     
>>>     model = Sequential()
>>>     model.add(Dense(128, input_shape=(X_train.shape[1],), init='uniform')) 
>>>     model.add(Activation('relu'))
>>>     model.add(Dropout(0.5))
>>>     model.add(Dense(1, init='uniform'))
>>>     model.add(Activation('sigmoid'))
>>>     model.summary()
>>>     model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
>>>    
>>>     start_time = time.time()
>>>     model.fit(X_train, y_train ,batch_size=batch_size, epochs=epochs, verbose=1, class_weight=class_weight)
>>>     end_time = time.time()
>>>     time_k[k] = end_time-start_time>>>     y_pred = model.predict_proba(X_test).round().astype(int)
>>>     y_train_pred = model.predict_proba(X_train).round().astype(int)
>>>     test_F1[k] = sklearn.metrics.f1_score(y_test, y_pred)
>>>     k += 1
>>> print ('Average Test f1-score', np.mean(test_F1))
Average Test f1-score 0.5236467236467236>>> print ('Average Run time', np.mean(time_k))
Average Run time 9.076935768127441

This was a difficult data to classify. To have a loose benchmark, let’s build a fancier LSTM classifier on the same data.

>>> X = darpa_data['seq']
>>> encoded_X = np.ndarray(shape=(len(X),), dtype=list)
>>> for i in range(0,len(X)):
>>>     encoded_X[i]=X.iloc[i].split("~")
>>> max_seq_length = np.max(darpa_data['seqlen'])
>>> encoded_X = sequence.pad_sequences(encoded_X, maxlen=max_seq_length)>>> kfold = 3
>>> random_state = 11>>> test_F1 = np.zeros(kfold)
>>> time_k = np.zeros(kfold)>>> epochs = 50
>>> batch_size = 15
>>> skf = StratifiedKFold(n_splits=kfold, shuffle=True, random_state=random_state)
>>> k = 0>>> for train_index, test_index in skf.split(encoded_X, y):
>>>     X_train, X_test = encoded_X[train_index], encoded_X[test_index]
>>>     y_train, y_test = y[train_index], y[test_index]
>>> 
>>>     embedding_vecor_length = 32
>>>     top_words=50
>>>     model = Sequential()
>>>     model.add(Embedding(top_words, embedding_vecor_length, input_length=max_seq_length))
>>>     model.add(LSTM(32))
>>>     model.add(Dense(1, init='uniform'))
>>>     model.add(Activation('sigmoid'))
>>>     model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])>>>     start_time = time.time()
>>>     model.fit(X_train, y_train, epochs=epochs, batch_size=batch_size, verbose=1)
>>>     end_time=time.time()
>>>     time_k[k]=end_time-start_time>>>     y_pred = model.predict_proba(X_test).round().astype(int)
>>>     y_train_pred=model.predict_proba(X_train).round().astype(int)
>>>     test_F1[k]=sklearn.metrics.f1_score(y_test, y_pred)
>>>     k+=1>>> print ('Average Test f1-score', np.mean(test_F1))
Average Test f1-score 0.0>>> print ('Average Run time', np.mean(time_k))
Average Run time 425.68603706359863

We find that the LSTM classifier gives an F1 score of 0. This may be improved by changing the model. However, we find that the SGT embedding could work with small and unbalanced data without the need of a complicated classifier. Besides, on the runtime, SGT embedded network was significantly faster. It took on average 9.1 secs while the LSTM model took 425.6 secs.

Concluding Remarks

• We learned about using a sequence embedding for sequence clustering and classification.
• This embedding is an implementation of this paper. Not covered in this post, but refer to this paper to see the accuracy comparison of SGT embedding over others.
• Due to SGT embedding’s ability to capture long- and short- term patterns, it works better than most other sequence modeling approaches.
• It is recommended that you play with the tuning parameter, kappa, to see its effect on accuracy.