In this post, we will learn about using a nonlinear correlation estimation function in R. We will also look at a few examples.

Background

Correlation estimations are commonly used in various data mining applications. In my experience, nonlinear correlations are quite common in various processes. Due to this, nonlinear models, such as SVM, are employed for regression, classification, etc. However, there are not many approaches to estimate nonlinear correlations between two variables.

Typically linear correlations are estimated. However, the data may have a nonlinear correlation but little to no linear correlation. In such cases, nonlinearly correlated variables are sometimes overlooked during data exploration or variable selection in high-dimensional data.

We have developed a new nonlinear correlation estimator:

nlcor

This estimator comes useful in data exploration and also variable selection for nonlinear predictive models, such as SVM.

Installing

To install

nlcor

 in R, follow these steps:

1. Install the devtools package. You can do this from CRAN. You can do it directly in R console by typing,

> install.packages("devtools")

2. Load the devtools package.

> library(devtools) 

3. Install

nlcor

from its GitHub repository by typing this in R console.

> install_github("ProcessMiner/nlcor")

Nonlinear Correlation Estimator: Nlcor

In this package, we provide an implementation of a nonlinear correlation estimation method using an adaptive local linear correlation computation in 

nlcor

The function

nlcor

returns the nonlinear correlation estimate, the corresponding adjusted p-value, and an optional plot visualizing the nonlinear relationships.

The correlation estimate will be between 0 and 1. The higher the value the more is the nonlinear correlation. Unlike linear correlations, a negative value is not valid here. Due to multiple local correlation computations, the net p-value of the correlation estimate is adjusted (to avoid false positives). The plot visualizes the local linear correlations.

In the following, we will show its usage with a few examples. In the given examples, the linear correlations between 

x

and

nlcor

is small, however, there is a visible nonlinear correlation between them. This package contains the data for these examples and can be used for testing the package.

nlcor

package has few sample

x

and

y

vectors that are demonstrated in the following examples.

First, we will load the package.

> library(nlcor)

Example 1. A data with cyclic nonlinear correlation.

> plot(x1, y1)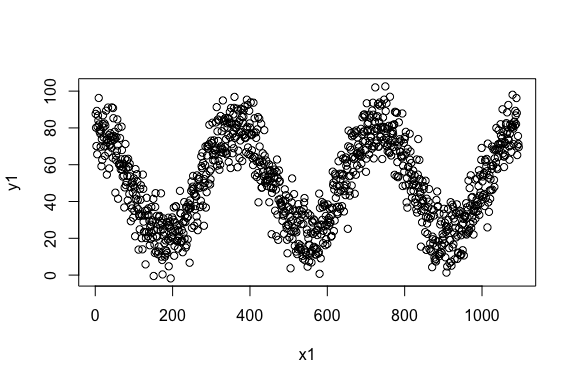

The linear correlation of the data is,

> cor(x1, y1)
[1] 0.008001837

As expected, the correlation is close to zero. We estimate the nonlinear correlation using 

nlcor

> c <- nlcor(x1, y1, plt = T)
> c$cor.estimate
[1] 0.8688784
> c$adjusted.p.value
[1] 0
> print(c$cor.plot)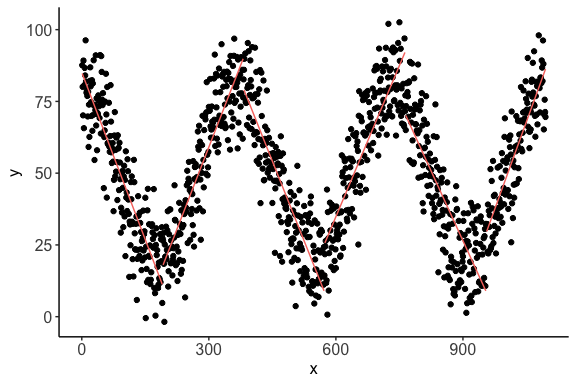

The plot shows the piecewise linear correlations present in the data.

Example 2. A data with non-uniform piecewise linear correlations.

> plot(x2, y2)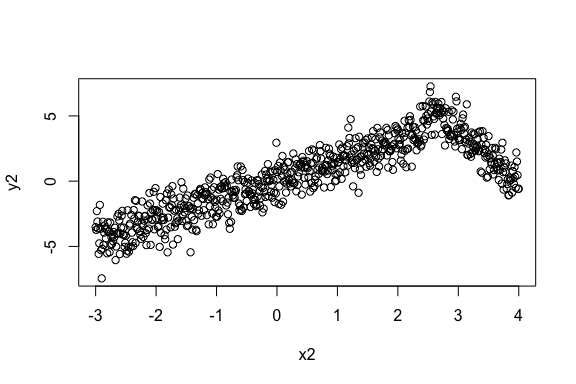

The linear correlation of the data is,

> cor(x2, y2)
[1] 0.828596

The linear correlation is quite high in this data. However, there is significant and higher nonlinear correlation present in the data. This data emulates the scenario where the correlation changes its direction after a point. Sometimes that change point is in the middle causing the linear correlation to be close to zero. Here we show an example when the change point is off-center to show that the implementation works in non-uniform cases.

We estimate the nonlinear correlation using 

nlcor

> c <- nlcor(x2, y2, plt = T)
> c$cor.estimate
[1] 0.897205
> c$adjusted.p.value
[1] 0
> print(c$cor.plot)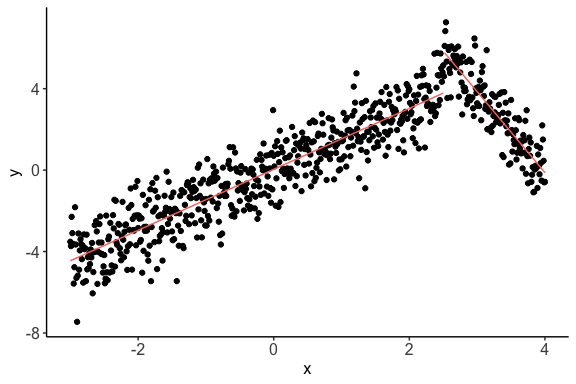

It is visible from the plot that 

nlcor

could estimate the piecewise correlations in a non-uniform scenario. Also, the nonlinear correlation comes out to be higher than the linear correlation.

Example 3. A data with higher and multiple frequency variations.

> plot(x3, y3)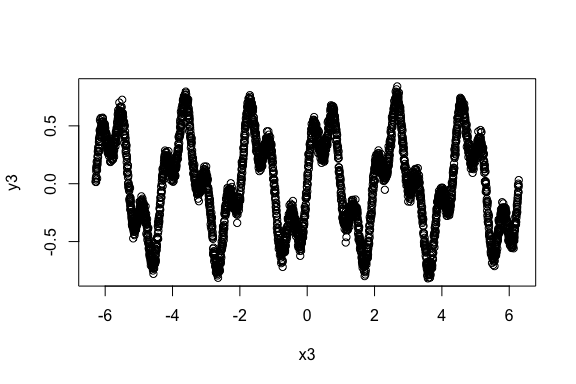

The linear correlation of the data is,

> cor(x3, y3)
[1] -0.1337304

The linear correlation is expectedly small, albeit not close to zero due to some linearity.

Here we show we can refine the granularity of the correlation computation.

Under default settings, the output of

nlcor

will be

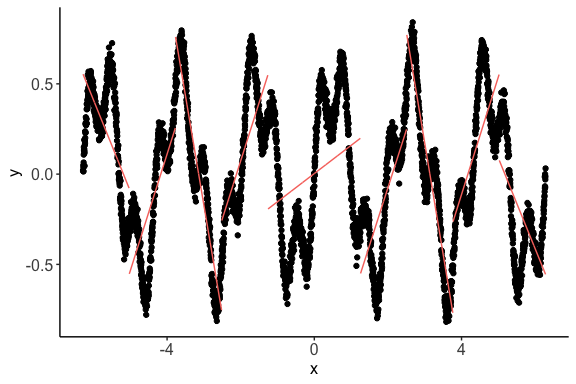
> c <- nlcor(x3, y3, plt = T)
> c$cor.estimate
[1] 0.7090148
> c$adjusted.p.value
[1] 0
> print(c$cor.plot)

As can be seen in the figure, 

nlcor

could identify the granular piecewise correlations. In this data, the p-value still remains extremely small—the correlation is statistically significant.

Summary